堆常用来实现优先队列,在这种队列中,待删除的元素为优先级最高(最低)的那个。在任何时候,任意优先元素都是可以插入到队列中去的,是计算机科学中一类特殊的数据结构的统称
一、堆的定义
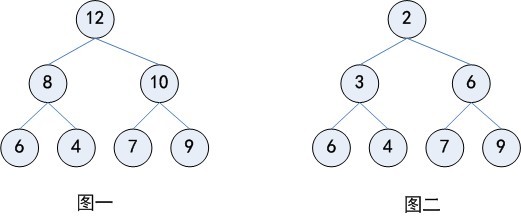
最大(最小)堆是一棵每一个节点的键值都不小于(大于)其孩子(如果存在)的键值的树。大顶堆是一棵完全二叉树,同时也是一棵最大树。小顶堆是一棵完全完全二叉树,同时也是一棵最小树。
注意:
- 堆中任一子树亦是堆。
- 以上讨论的堆实际上是二叉堆(Binary Heap),类似地可定义k叉堆。
下图分别给出几个最大堆和最小堆的例子:
二、支持的基本操作
堆支持以下的基本操作:
- build: 建立一个空堆;
- insert: 向堆中插入一个新元素;
- update:将新元素提升使其符合堆的性质;
- get:获取当前堆顶元素的值;
- delete:删除堆顶元素;
- heapify:使删除堆顶元素的堆再次成为堆。
某些堆实现还支持其他的一些操作,如斐波那契堆支持检查一个堆中是否存在某个元素。
三、堆的应用
1.堆排序
堆排序(HeapSort)是一树形选择排序。
堆排序的特点是:在排序过程中,将R[l..n]看成是一棵完全二叉树的顺序存储结构,利用完全二叉树中双亲结点和孩子结点之间的内在关系【参见二叉树的顺序存储结构】,在当前无序区中选择关键字最大(或最小)的记录。
优点直接选择排序中,为了从R[1..n]中选出关键字最小的记录,必须进行n-1次比较,然后在R[2..n]中选出关键字最小的记录,又需要做n-2次比较。事实上,后面的n-2次比较中,有许多比较可能在前面的n-1次比较中已经做过,但由于前一趟排序时未保留这些比较结果,所以后一趟排序时又重复执行了这些比较操作。
堆排序可通过树形结构保存部分比较结果,可减少比较次数。
堆排序利用了大根堆(或小根堆)堆顶记录的关键字最大(或最小)这一特征,使得在当前无序区中选取最大(或最小)关键字的记录变得简单。
(1)、用大根堆排序的基本思想
- 先将初始文件R[1..n]建成一个大根堆,此堆为初始的无序区
- 再将关键字最大的记录R[1](即堆顶)和无序区的最后一个记录R[n]交换,由此得到新的无序区R[1..n-1]和有序区R[n],且满足R[1..n-1].keys≤R[n].key
- 由于交换后新的根R[1]可能违反堆性质,故应将当前无序区R[1..n-1]调整为堆。然后再次将R[1..n-1]中关键字最大的记录R[1]和该区间的最后一个记录R[n-1]交换,由此得到新的无序区R[1..n-2]和有序区R[n-1..n],且仍满足关系R[1..n-2].keys≤R[n-1..n].keys,同样要将R[1..n-2]调整为堆。直到无序区只有一个元素为止。
(2)、大根堆排序算法的基本操作:
- 初始化操作:将R[1..n]构造为初始堆;
- 每一趟排序的基本操作:将当前无序区的堆顶记录R[1]和该区间的最后一个记录交换,然后将新的无序区调整为堆(亦称重建堆)。
注意:
- 只需做n-1趟排序,选出较大的n-1个关键字即可以使得文件递增有序。
- 用小根堆排序与利用大根堆类似,只不过其排序结果是递减有序的。堆排序和直接选择排序相反:在任何时刻,堆排序中无序区总是在有序区之前,且有序区是在原向量的尾部由后往前逐步扩大至整个向量为止。
(3)、算法实现
////////////////////////////////////////////////////////////////////
//堆排序
template <class T>
void Sort::HeapSort(T arr[], int len){
int i;
//建立子堆
for(i = len / 2; i >= 1; i--){
CreateHeap(arr, i, len);
}
for(i = len - 1; i >= 1; i--){
buff = arr[1];
arr[1] = arr[i + 1];
arr[i + 1] = buff;
CreateHeap(arr, 1, i);
}
}
//建立堆
template <class T>
void Sort::CreateHeap(T arr[], int root, int len){
int j = 2 * root; //root's left child, right (2 * root + 1)
T temp = arr[root];
bool flags = false;
while(j <= len && !flags){
if(j < len){
if(arr[j] < arr[j + 1]){ // Left child is less then right child
++j; // Move the index to the right child
}
}
if(temp < arr[j]){
arr[j / 2] = arr[j];
j *= 2;
}else{
flags = true;
}
}
arr[j / 2] = temp;
} 2.选择前k个最大(最小)的数
思想:在一个很大的无序数组里面选择前k个最大(最小)的数据,最直观的做法是把数组里面的数据全部排好序,然后输出前面最大(最小)的k个数据。但是,排序最好需要O(nlogn)的时间,而且我们不需要前k个最大(最小)的元素是有序的。这个时候我们可以建立k个元素的最小堆(得出前k个最大值)或者最大堆(得到前k个最小值),我们只需要遍历一遍数组,在把元素插入到堆中去只需要logk的时间,这个速度是很乐观的。利用堆得出前k个最大(最小)元素特别适合海量数据的处理。
代码:
typedef multiset<int, greater<int> > intSet;
typedef multiset<int, greater<int> >::iterator setIterator;
void GetLeastNumbers(const vector<int>& data, intSet& leastNumbers, int k)
{
leastNumbers.clear();
if(k < 1 || data.size() < k)
return;
vector<int>::const_iterator iter = data.begin();
for(; iter != data.end(); ++ iter)
{
if((leastNumbers.size()) < k)
leastNumbers.insert(*iter);
else
{
setIterator iterGreatest = leastNumbers.begin();
if(*iter < *(leastNumbers.begin()))
{
leastNumbers.erase(iterGreatest);
leastNumbers.insert(*iter);
}
}
}
} 本博客文章除特别声明,全部都是原创!原创文章版权归过往记忆大数据(过往记忆)所有,未经许可不得转载。
本文链接: 【数据结构:堆】(https://www.iteblog.com/archives/97.html)