斐波那契数列又译费波拿契数、斐波那契数列、费氏数列、黄金分割数列。
根据高德纳(Donald Ervin Knuth)的《计算机程序设计艺术》(The Art of Computer Programming),1150年印度数学家Gopala和金月在研究箱子包装物件长阔刚好为 1 和 2 的可行方法数目时,首先描述这个数列。 在西方,最先研究这个数列的人是比萨的列奥那多(又名费波那西),他描述兔子生长的数目时用上了这数列。
- 第一个月初有一对刚诞生的兔子
- 第二个月之后(第三个月初)它们可以生育
- 每月每对可生育的兔子会诞生下一对新兔子
- 兔子永不死去
假设在 n 月有可生育的兔子总共 a 对,n+1 月就总共有 b 对。在 n+2 月必定总共有 a+b 对: 因为在 n+2 月的时候,前一月(n+1月)的 b 对兔子可以存留至第n+2月(在当月属于新诞生的兔子尚不能生育)。而新生育出的兔子对数等于所有在 n 月就已存在的 a 对
用数学公式表示就是:
a1=1;
a2=1;
an = an-1 + an-2 其中n>2
这个等式就是大学刚刚学递归的时候学习的,因为这个很容易用递归的代码实现,很简单:
// Author: 过往记忆
// Email: wyphao.2007@163.com
// Blog:www.iteblog.com
// 仅用于学习,转载请注明出处
long Fibonacci(int n){
if (n==0) return 1;
if (n==1) return 1;
if (n>1) return Fibonacci(n-1) + Fibonacci(n-2);
}
代码简单,明了。但是仔细分析会发现,在算Fibonacci(n)的时候,需要用到Fibonacci(n-1)和Fibonacci(n-2),但是Fibonacci(n-1)的计算依赖于Fibonacci(n-2)和Fibonacci(n-3),这样需要一直计算下去,会有很多重复的计算,因为递归没有保存下中间的计算过程。如下图所示: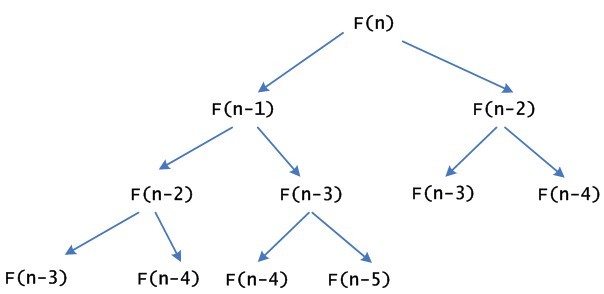
这种时间复杂度很高差不多是5n^2/3。
既然在递归的过程中没有保存下中间的计算过程,我们可以声明一个数组用于保存中间的计算过程,在每一次递归之前,先判断数组里面是否有Fibonacci(n)的值;如果有,那就直接取出返回;如果没有。则递归计算一次,然后把计算出来的Fibonacci(n)值保存在数组中,以便于下次使用。算法如下所示:
#include <stdio.h>
// Author: 过往记忆
// Email: wyphao.2007@163.com
// Blog:www.iteblog.com
// 仅用于学习,转载请注明出处
long long temp[100] = {0};
long long Fibonacci(int n){
if(n == 1){
return 1;
}
if(n == 2){
return 1;
}
if(temp[n] != 0){
return temp[n];
}else{
long long sum = Fibonacci(n - 1) + Fibonacci(n - 2);
temp[n] = sum;
return sum;
}
}
int main(){
printf("%d\n", Fibonacci(21));
return 0;
}
上面的方法也是利用递归实现的,但是在计算的过程中,保存下中间的计算过程,所以计算速度明显比上面的块多了。
但是递归终究是递归,它的效率终究是比较低的,那么,我们可以用非递归的方法来解决递归效率慢的问题,可以同样用数字保存中间的计算过程,如下所示:
// Author: 过往记忆
// Email: wyphao.2007@163.com
// Blog:www.iteblog.com
// 仅用于学习,转载请注明出处
int Fibonacci2(int n){
if(n < 1){
return -1;
}
if(n < 3){
return 1;
}
int *a =new int[n];
*a=*(a+1)=1;
for(int i=2;i<n;i++){
a[i]=a[i-1]+a[i-2];
}
int temp = a[n-1];
delete a;//释放内存(一个new对应一个delete)
return temp;
}
这种方法速度很快,但是在计算过程中用了很多的空间(int *a =new int[n];),能不能不申请这么多的空间呢?答案是可以的,因为每一次计算值用到了前两个值,所以,我们可以值申请两个临时变量用以保存前面的两个值,代码实现如下:
#include <iostream>
using namespace std;
// Author: 过往记忆
// Email: wyphao.2007@163.com
// Blog:www.iteblog.com
// 仅用于学习,转载请注明出处
unsigned long long Fibonacci(int n){
unsigned long long first = 0, second = 1;
unsigned long long tempSum = 0;
int i =0;
if(n == 0){
return 0;
}else if(n == 1){
return 1;
}
for(i = 2; i <= n; i++){
tempSum = first + second;
first = second;
second = tempSum;
}
return tempSum;
}
int main(){
int n;
while(cin >> n){
cout << Fibonacci(n) << endl;
}
return 0;
}
这种方法非常的高效。在实际的面试中,面试官很少直接问你斐波那契数列,而是直接问题一些别的东西,比如:
青蛙跳台阶问题
一只青蛙一次可以跳上1级台阶,也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法
分析:首先我们考虑最简单的情况。如果只有1级台阶,那显然只有一种跳法。如果有2级台阶,那就有两种跳的方法了:一种是分两次跳,每次跳1级;另外一种就是一次跳2级。 现在我们再来讨论一般情况。我们把n级台阶时的跳法看成是n的函数,记为f(n)。当n>2时,第一次跳的时候就有两种不同的选择:一是第一次只跳1级,此时跳法数目等于后面剩下的n-1级台阶的跳法数目,即为f(n-1);另外一种选择是第一次跳2级,此时跳法数目等于后面剩下的n-2级台阶的跳法数目,即为f(n-2)。因此n级台阶时的不同跳法的总数f(n)=f(n-1)+(f-2)。
我们把上面的分析用一个公式总结如下:
f(1) = 1 n=1
f(2) = 2 n=2
f(n) = f(n-1)+(f-2) n>2
所以这是一个很典型的斐波那契数列。直接用上面的方法就可以实现。
还有一些例子,比如:
变态跳台阶
一只青蛙一次可以跳上1级台阶,也可以跳上2级……它也可以跳上n级。求该青蛙跳上一个n级的台阶总共有多少种跳法。
其实也是一个变形的斐波那契数列。分析:
分析:用Fib(n)表示青蛙跳上n阶台阶的跳法数,青蛙一次性跳上n阶台阶的跳法数1(n阶跳),设定Fib(0) = 1;
- 当n = 1 时, 只有一种跳法,即1阶跳:Fib(1) = 1;
- 当n = 2 时, 有两种跳的方式,一阶跳和二阶跳:Fib(2) = Fib(1) + Fib(0) = 2;
- 当n = 3 时,有三种跳的方式,第一次跳出一阶后,后面还有Fib(3-1)中跳法; 第一次跳出二阶后,后面还有Fib(3-2)中跳法;第一次跳出三阶后,后面还有Fib(3-3)中跳法Fib(3) = Fib(2) + Fib(1)+Fib(0)=4;
- 当n = n 时,共有n种跳的方式,第一次跳出一阶后,后面还有Fib(n-1)中跳法; 第一次跳出二阶后,后面还有Fib(n-2)中跳法。第一次跳出n阶后,后面还有 Fib(n-n)中跳法.
Fib(n) = Fib(n-1)+Fib(n-2)+Fib(n-3)+...+Fib(n-n)=Fib(0)+Fib(1)+Fib(2)+...+Fib(n-1)
又因为Fib(n-1)=Fib(0)+Fib(1)+Fib(2)+...+Fib(n-2)
两式相减得:Fib(n)-Fib(n-1)=Fib(n-1) =====》 Fib(n) = 2*Fib(n-1) n >= 2
所以可以得到的递推公式为:
fib(1) = 1 n=1
fib(2) = 2 n=2
fib(n) = 2*Fib(n-1) n >= 2
实现
#include <iostream>
using namespace std;
// Author: 过往记忆
// Email: wyphao.2007@163.com
// Blog:www.iteblog.com
// 仅用于学习,转载请注明出处
int main()
{
long long f[51]={0,1,2},n = 3,sum = 3;
for(int i = 3;i <= 50 ;i++) {
f[i] = sum + 1;
sum += f[i];
}
while(cin >> n){
cout << f[n] << endl;
}
return 0;
}
当然还有很多的斐波那契数列变形,其实善于分析,就可以很好的解决这类的问题。
本博客文章除特别声明,全部都是原创!原创文章版权归过往记忆大数据(过往记忆)所有,未经许可不得转载。
本文链接: 【面试中几种常见的斐波那契数列模型】(https://www.iteblog.com/archives/268.html)







